The KV Cache

The computation of attention is costly. Remember that our decoder works in an auto-regressive fashion. For our given input $$\colorbox{red}{What}\colorbox{magenta}{ is}\colorbox{green}{ the}\colorbox{orange}{ capital}\colorbox{purple}{ of}\colorbox{brown}{ France}\colorbox{cyan}{?}"$$

\begin{align} \text{Prediction 1} &= \colorbox{orange}{The} \\ \text{Prediction 2} &= \colorbox{orange}{The}\colorbox{pink}{ capital} \\ &\vdots \\ \text{Prediction $p$} &= \colorbox{orange}{The}\colorbox{pink}{ capital} (\dots) \colorbox{red}{ Paris.} \end{align}

To produce prediction $2$, we will take the output from prediction $1$. At each step, the model will also see our input sequence. Without any tricks, at every step, we’re going to be re-computing values that have already been calculated. Our attention matrix used for our first prediction will have the following structure

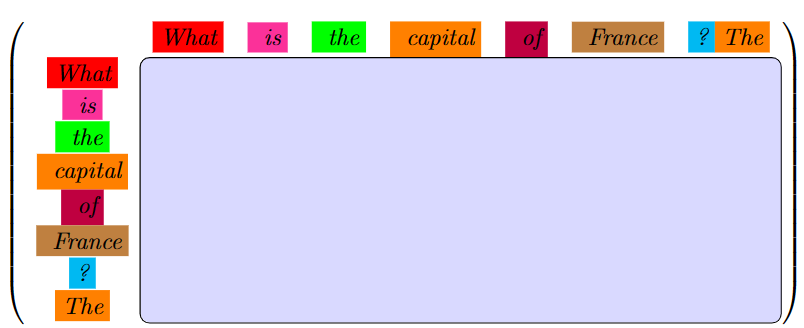
When we compute the second prediction, the structure of our attention matrix looks very similar. Notice that the attention matrix after prediction one is actually contained within this matrix!

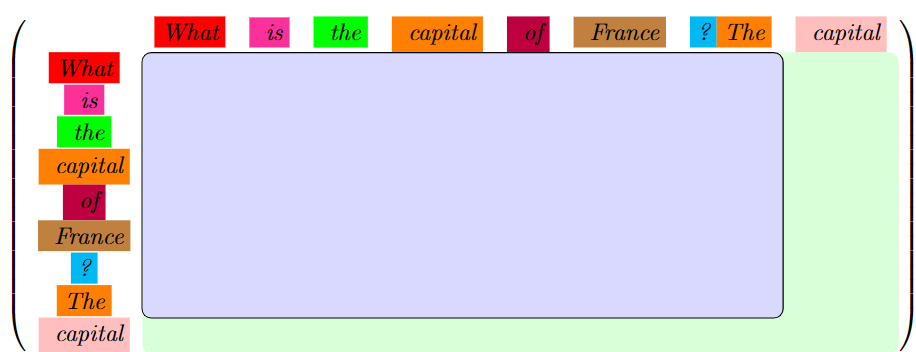
Remember, $Q$ and $K^T$ are just defined by our matrix $M$ which contains one row per input token. Thus, $Q$ and $K^T$ are very similar between the first and second predictions - only one row / column has changed! By caching $K$ for each prediction, we can make the computation of our attention matrix more efficient and by caching $V$, we make our attention mechanism output calculation more efficient.